2024 AMC 10A solutions

2024 AMC 10A Problem 1

Problem:
What is the value of $101\cdot 9,901-99\cdot 10,101$ ?

Answer Choices:

A. $2$

B. $20$

C. $21$

D. $200$

E. $2020$

Solution:

Write the difference as

$$(100+1)\cdot (9900+1)-99\cdot (10,000+100+1)\mathrm{.}$$

Applying the distributive property gives

$$(990,000+9,900+100+1)-(990,000+9,900+99)=100+1-99=(\text{A})\boxed{{\displaystyle 2}}\mathrm{.}$$

$$\mathbf{\text{OR}}$$

Let $x=100$. Then the minuend (the first quantity in the subtraction operation) is

$$(x+1)(x^2-x+1)=x^3+1,$$

and the subtrahend (the quantity being subtracted from the minuend) is

$$(x-1)(x^2+x+1)=x^3-1.$$

The difference is

$$(x^3+1)-(x^3-1)=(\text{A})\boxed{{\displaystyle 2}}\mathrm{.}$$

 

2024 AMC 10A Problem 2

Problem:
A model used to estimate the time it will take to hike to the top of a mountain on a trail is of the form $T=aL+bG$, where $a$ and $b$ are constants, $T$ is the time in minutes, $L$ is the length of the trail in miles, and $G$ is the altitude gain in feet. The model estimates that it will take 69 minutes to hike to the top if a trail is 1.5 miles long and ascends 800 feet, as well as if a trail is 1.2 miles long and ascends 1100 feet. How many minutes does the model estimate it will take to hike to the top if the trail is 4.2 miles long and ascends 4000 feet?

Answer Choices:

A. $240$

B. $246$

C. $252$

D. $258$

E. $264$

Solution:

The given data from the first two hikes yield the system of equations

$$\begin{array}{cc}{\displaystyle 1.5a+800b}& {\displaystyle =69}\\ {\displaystyle 1.2a+1100b}& {\displaystyle =69.}\end{array}$$

To solve this system, first subtract the second equation from the first equation to get $0.3a-300b=0$, which implies $a=1000b$. Then the first equation becomes $1500b+800b=69$, from which $b=\frac{69}{2300}=0.03$, and $a=30$. Therefore the model is $T=30L+0.03G$. Substituting the values for the third hike gives $T=30\cdot 4.2+0.03\cdot 4000=(\text{B})\boxed{{\displaystyle 246}}$ minutes.

Note: Expressed in words, this commonly used model is "two miles per hour plus a half-hour for each 1000 feet of altitude gain."

2024 AMC 10A Problem 3

Problem:
Let $n$ be the least prime number that can be written as the sum of 5 distinct prime numbers. What is the sum of the digits of $n$ ?

Answer Choices:

A. $5$

B. $7$

C. $8$

D. $10$

E. $11$

Solution:

The prime 2 cannot be among the 5 distinct primes chosen because, if it were, then the sum would be even. The first 5 odd primes are $3,5,7,11$, and 13 , and their sum is 39 , which is not prime. The next smallest sum of 5 distinct odd primes is $3+5+7+11+17=43$, which is prime. The requested digit sum is $4+3=(\text{B})\boxed{{\displaystyle 7}}$.

2024 AMC 10A Problem 4

Problem:
The number 2024 is written as the sum of not necessarily distinct two-digit numbers. What is the least number of two-digit numbers needed to write this sum?

Answer Choices:

A. $20$

B. $21$

C. $22$

D. $23$

E. $24$

Solution:

In order to minimize the number of terms in the sum, the greatest two-digit number, 99 , should be used as many times as possible. Because $20\cdot 99=1980$, the minimum number of terms is greater than 20 . On the other hand, $2024=20\cdot 99+44$, so the least number of two-digit numbers needed is $(\text{B})\boxed{{\displaystyle 21}}$.

2024 AMC 10A Problem 5

Problem:
What is the least value of $n$ such that $n$ ! is a multiple of 2024 ?

Answer Choices:

A. $11$

B. $21$

C. $22$

D. $23$

E. $253$

Solution:

Because the prime factorization of 2024 is $2^3\cdot 11\cdot 23$, it follows that $n!$ is a multiple of 2024 if and only if $n\ge 23$. Therefore $(\text{B})\boxed{{\displaystyle 23}}$ is the least value of $n$ such that $n!$ is a multiple of 2024 .

2024 AMC 10A Problem 6

Problem:
What is the minimum number of successive swaps of adjacent letters in the string ABCDEF that are needed to change the string to FEDCBA ? (For example, 3 swaps are required to change ABC to CBA ; one such sequence of swaps is $\mathrm{A}\mathrm{B}\mathrm{C}\to \mathrm{B}\mathrm{A}\mathrm{C}\to \mathrm{B}\mathrm{C}\mathrm{A}\to \mathrm{C}\mathrm{B}\mathrm{A}$.)

Answer Choices:

A. $6$

B. $10$

C. $12$

D. $15$

E. $24$

Solution:

If the A is swapped 5 times, once with each of the other letters, the result will be BCDEFA. Now the B can be swapped 4 times in the same way to end up in the fifth position: CDEFBA. Continuing in this way gives a sequence of $5+4+3+2+1=15$ swaps that achieves the required result.

To see that no sequence of fewer than 15 swaps will work, note that in ABCDEF there are 15 instances of pairs of letters that are in alphabetical order $(\mathrm{A}\mathrm{B},\mathrm{A}\mathrm{C},\dots ,\mathrm{A}\mathrm{F},\mathrm{B}\mathrm{C},\mathrm{B}\mathrm{D},\dots \mathrm{B}\mathrm{F},\dots ,\mathrm{E}\mathrm{F})$, and in the required final string there are no such pairs. Each swap can decrease the number of pairs of letters that are in alphabetical order by just 1 , so at least $(\text{D})\boxed{{\displaystyle 15}}$ swaps are required.

Note: The method described in the problem is called the "bubble sort" algorithm.

2024 AMC 10A Problem 7

Problem:
The product of three integers is 60. What is the least possible positive sum of the three integers?

Answer Choices:

A. $2$

B. $3$

C. $5$

D. $6$

E. $13$

Solution:

Note that $60=10\cdot (-1)\cdot (-6)$, and the sum of these factors is $(\text{B})\boxed{{\displaystyle 3}}$. It remains to show that no positive sum can be less than 3 . Such a sum would have to consist of one positive integer and two negative integers with smaller absolute value. If the positive integer is greater than or equal to 10 , then the sum is greater than or equal to 3 . The possible sets of factors in this case are $\{10,-6,-1\},\{10,-3,-2\},\{12,-5,-1\},\{15,-4,-1\},\{15,-2,-2\},\{20,-3,-1\},\{30,-2,-1\}$,

 and $\{60,-1,-1\}$. None of these sets of factors has a sum less than 3 .

The only other possible choices for the positive integer are 5 and 6 , and in neither case is a positive sum possible. Indeed, if the positive integer is 5 , then the only possible set of factors is $\{5,-3,-4\}$. If the positive integer is 6 , then the only possible set of factors is $\{6,-5,-2\}$. In both of these cases, the sum is not positive.

2024 AMC 10A Problem 8

Problem:
Amy, Bomani, Charlie, and Daria work in a chocolate factory. On Monday Amy, Bomani, and Charlie started working at 1:00 PM and were able to pack 4, 3, and 3 packages, respectively, every 3 minutes. At some later time, Daria joined the group, and Daria was able to pack 5 packages every 4 minutes. Together, they finished packing 450 packages at exactly $2:45\mathrm{P}\mathrm{M}$. At what time did Daria join the group?

Answer Choices:

A. $1:25\mathrm{P}\mathrm{M}$

B. $1:35\mathrm{P}\mathrm{M}$

C. $1:45\mathrm{P}\mathrm{M}$

D. $1:55\mathrm{P}\mathrm{M}$

E. $2:05\mathrm{P}\mathrm{M}$

Solution:

Every 3 minutes, Amy, Bomani, and Charlie together packed 10 packages. From 1:00 PM to $2:45\mathrm{P}\mathrm{M}$, a span of $60+45=105$ minutes, these three packers packed $\frac{105}{3}\cdot 10=350$ packages. This means that Daria must have packed $450-350=100$ packages. The time needed for Daria to pack 100 packages is $\frac{100}{5}\cdot 4=80$ minutes. Therefore Daria joined the group at $(\text{B})\boxed{{\displaystyle 1:25\mathrm{P}\mathrm{M}}}$, which is 80 minutes before $2:45\mathrm{P}\mathrm{M}$.

2024 AMC 10A Problem 9

Problem:
In how many ways can 6 juniors and 6 seniors form 3 disjoint teams of 4 people so that each team has 2 juniors and 2 seniors?

Answer Choices:

A. $720$

B. $1350$

C. $2700$

D. $3280$

E. $8100$

Solution:

Select the first junior and call this person $A$. There are 5 other juniors and $\left(\genfrac{}{}{0px}{}{6}{2}\right)=15$ pairs of seniors who could team up with $A$. Select the next junior not yet on a team, say $B$. There are 3 other juniors and $\left(\genfrac{}{}{0px}{}{4}{2}\right)=6$ pairs of seniors who could team up with $B$. The third team consists of the people not yet chosen. Thus there are $5\cdot 15\cdot 3\cdot 6=(\text{B})\boxed{{\displaystyle 1350}}$ ways to form the teams.

$$\mathbf{\text{OR}}$$

There are $\left(\genfrac{}{}{0px}{}{6}{2,2,2}\right)=\frac{6!}{2!2!2!}=90$ ways to assign the seniors to teams 1,2 , and 3 , and, similarly, 90 ways to assign juniors to those teams. But there are $3!=6$ ways for the three teams to be ordered, so the number of ways to form the teams is $\frac{90\cdot 90}{6}=(\text{B})\boxed{{\displaystyle 1350}}$.

2024 AMC 10A Problem 10

Problem:
Consider the following operation. Given a positive integer $n$, if $n$ is a multiple of 3 , then you replace $n$ by $\frac{n}{3}$. If $n$ is not a multiple of 3 , then you replace $n$ by $n+10$. Then continue this process. For example, beginning with $n=4$, this procedure gives $4\to 14\to 24\to 8\to 18\to 6\to 2\to 12\to \cdots$. Suppose you start with $n=100$. What value results if you perform this operation exactly 100 times?

Answer Choices:

A. $10$

B. $20$

C. $30$

D. $40$

E. $50$

Solution:

The first several iterations give

$$100\to 110\to 120\to 40\to 50\to 60\to 20\to 30\to 10\to 20\to 30\to 10\to \cdots$$

The values will then continue to cycle through $20\to 30\to 10$. Note that the value 20 occurs after $6,9,12,15,\dots$ operations; the value 30 occurs after $7,10,13,16,\dots$ operations; and the value 10 occurs after $8,11,14,17,\dots$ operations. Because 100 has remainder 1 when divided by 3 , the value after 100 operations is $(\text{c})\boxed{{\displaystyle 30}}$.

2024 AMC 10A Problem 11

Problem:
How many ordered pairs of integers $(m,n)$ satisfy $\sqrt{n^2-49}=m$ ?

Answer Choices:

A. $1$

B. $2$

C. $3$

D. $4$

E. infinitely many

Solution:

Notice that $m\ge 0$, and if $(m,n)$ is a solution, then so is $(m,-n)$. Assume $n\ge 0$. Squaring both sides of the given equation gives $n^2-49=m^2$, so $n^2-m^2=(n-m)(n+m)=49$. Because $n-m$ and $n+m$ are positive integers, either $n-m=n+m=7$, or $n-m=1$ and $n+m=49$. The first case gives $(0,7)$ as a solution, and the second case gives $(24,25)$ as a solution. Because $n$ is squared in the given equation, the corresponding negative values for $n$ also give solutions: $(0,-7)$ and $(24,-25)$. There are $(\text{D})\boxed{{\displaystyle 4}}$ solutions in all.

2024 AMC 10A Problem 12

Problem:
Zelda played the Adventures of Math game on August 1 and scored 1700 points. She continued to play daily over the next 5 days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was $1700+80=1780$ points.) What was Zelda's average score in points over the 6 days?

$$\mathbf{\text{Daily}}\mathbf{\text{Change}}\mathbf{\text{in}}\mathbf{\text{Score}}\mathbf{\text{from}}\mathbf{\text{August}}\mathbf{\text{2}}\mathbf{\text{to}}\mathbf{\text{6}}$$

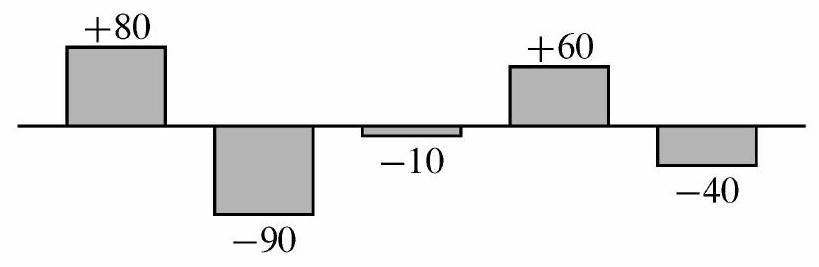
Aug 2 Aug 3 Aug 4 Aug 5 Aug 6
Answer Choices:

A. $1700$

B. $1702$

C. $1703$

D. $1713$

E. $1715$

Solution:

The table below shows Zelda's daily scores over the 6 days.

$$\begin{array}{ccc}\mathbf{\text{<br>}}& \mathbf{\text{Change}}& \mathbf{\text{Score}}\\ Aug1& & 1700\\ Aug2& +80& 1780\\ Aug3& -90& 1690\\ Aug4& -10& 1680\\ Aug5& +60& 1740\\ Aug6& -40& 1700\end{array}$$

Summing the scores and dividing by 6 gives an average of

$$\frac{1700+1780+1690+1680+1740+1700}{6}=\frac{10290}{6}=(\text{E})\boxed{{\displaystyle 1715}}\text{ points. }$$

$$\mathbf{\text{OR}}$$

The bar chart below shows the cumulative change in Zelda's score relative to the 1700 points scored on August 1.

$$\mathbf{\text{Cumulative}}\mathbf{\text{Change}}\mathbf{\text{in}}\mathbf{\text{Score}}\mathbf{\text{since}}\mathbf{\text{August}}\mathbf{\text{1}}$$

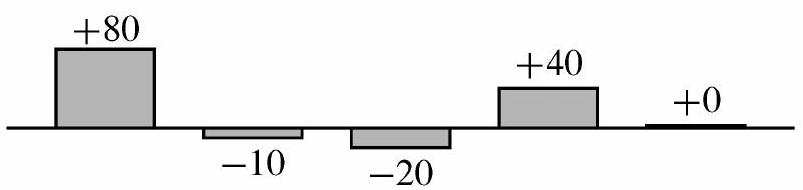
Aug 2 Aug 3 Aug $4$ Aug $5$ Aug 6

The average cumulative change over the 6 days was

$$\frac{80-10-20+40+0}{6}=\frac{90}{6}=15\text{ points }$$

so Zelda's average score over the 6 days was $1700+15=(\text{E})\boxed{{\displaystyle 1715}}$ points.

2024 AMC 10A Problem 13

Problem:
Two transformations are said to commute if applying the first followed by the second gives the same result as applying the second followed by the first. Consider these four transformations of the coordinate plane:

• A translation $2$ units to the right,
• A $90^{\circ }$-rotation counterclockwise about the origin,
• A reflection across the $x$-axis, and
• A dilation centered at the origin with scale factor 2 .

Of the 6 pairs of distinct transformations from this list, how many commute?

Answer Choices:

A. $1$

B. $2$

C. $3$

D. $4$

E. $5$

Solution:

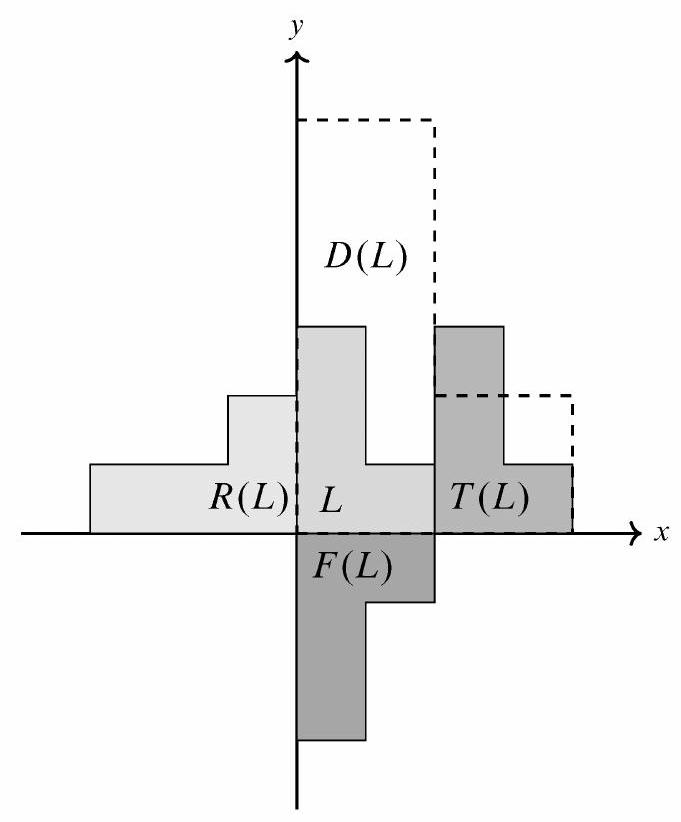
Denote the transformations by $T,R,F$, and $D$ in the order given in the problem statement. Then the images of point $(x,y)$ are $T(x,y)=(x+2,y),R(x,y)=(-y,x),F(x,y)=$ $(x,-y)$, and $D(x,y)=(2x,2y)$. The results of applying a pair of transformations in either order are as follows:

• $T(R(x,y))=T(-y,x)=(-y+2,x)$ and $R(T(x,y))=R(x+2,y)=(-y,x+2)$
• $(-y,x+2)$. The results are different, so $T$ and $R$ do not commute.
• $T(F(x,y))=T(x,-y)=(x+2,-y)$ and $F(T(x,y))=F(x+2,y)=(x+2,-y)$
• $(x+2,-y)$. The results are the same, so $T$ and $F$ do commute.
• $T(D(x,y))=T(2x,2y)=(2x+2,2y)$ and $D(T(x,y))=D(x+2,y)=(2x+4,2y)$
• $(2x+4,2y)$. The results are different, so $T$ and $D$ do not commute.
• $R(F(x,y))=R(x,-y)=(y,x)$ and $F(R(x,y))=F(-y,x)=(-y,-x)$
• $(-y,-x)$. The results are different, so $R$ and $F$ do not commute.
• $R(D(x,y))=R(2x,2y)=(-2y,2x)$ and $D(R(x,y))=D(-y,x)=(-2y,2x)$
• $(-2y,2x)$. The results are the same, so $R$ and $D$ do commute.
• $D(F(x,y))=D(x,-y)=(2x,-2y)$ and $F(D(x,y))=F(2x,2y)=(2x,-2y)$
• $(2x,-2y)$. The results are the same, so $D$ and $F$ do commute.

Thus $(\text{C})\boxed{{\displaystyle 3}}$ of the 6 pairs commute.

Note: The following figure illustrates the application of each transformation to an L-shaped figure.

2024 AMC 10A Problem 14

Problem:
One side of an equilateral triangle of height 24 lies on line $\mathrm{\ell }$. A circle of radius 12 is tangent to $\mathrm{\ell }$ and is externally tangent to the triangle. The area of the region exterior to the triangle and the circle and bounded by the triangle, the circle, and line $\mathrm{\ell }$ can be written as $a\sqrt{b}-c\pi$, where $a,b$, and $c$ are positive integers and $b$ is not divisible by the square of any prime. What is $a+b+c$ ?

Answer Choices:

A. $72$

B. $73$

C. $74$

D. $75$

E. $76$

Solution:

The given situation is shown in the figure below, where $D$ is the center of the circle, $E$ is the point of tangency between the circle and the triangle, $F$ is the intersection of line $DE$ with line $\mathrm{\ell }$, and $G$ is the projection of $D$ onto $\mathrm{\ell }$.

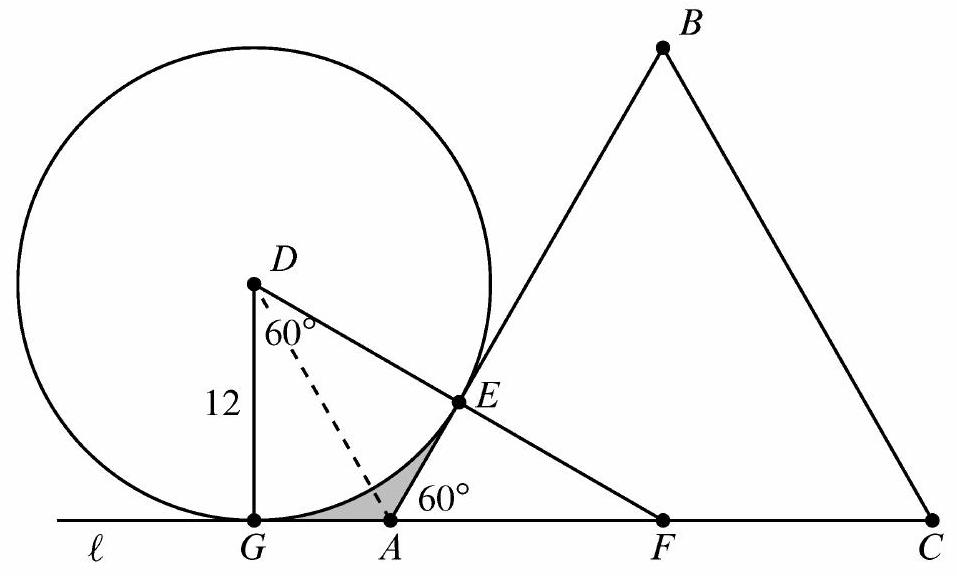
Because $\mathrm{\angle }BAC=60^{\circ }$ and $\mathrm{\angle }DEA=\mathrm{\angle }DGF=90^{\circ }$, both $\mathrm{△}AEF$ and $\mathrm{△}DGF$ are $30-60-90^{\circ }$ right triangles. Therefore $DF=24,EF=24-12=12,AE=4\sqrt{3},AF=8\sqrt{3},FG=12\sqrt{3}$, and $AG=12\sqrt{3}-8\sqrt{3}=4\sqrt{3}$. The area of kite $GAED$ is twice the area of $\mathrm{△}GAD$, so it is $48\sqrt{3}$. The area of the $60^{\circ }$-sector $EDG$ of the circle is $\frac{1}{6}\cdot \pi \cdot 12^2=24\pi$. Thus the required area, shaded in the figure, is $48\sqrt{3}-24\pi$, and the requested sum is $48+3+24=(\text{B})\boxed{{\displaystyle 75}}$.

$$\mathbf{\text{OR}}$$

The required area is $\frac{1}{6}$ of the difference between the area of a circle of radius 12 and a circumscribed regular hexagon. The hexagon is the union of 6 equilateral triangles of side length $s=12\cdot \frac{2}{\sqrt{3}}$. The area of the hexagon is $6\cdot \frac{\sqrt{3}}{4}{s}^2$, which equals $288\sqrt{3}$. The area of the circle is $144\pi$. Then $\frac{1}{6}$ of the difference is $48\sqrt{3}-24\pi$, and the requested sum is $48+3+24=(\text{B})\boxed{{\displaystyle 75}}$.

2024 AMC 10A Problem 15

Problem:
Let $M$ be the greatest integer such that both $M+1213$ and $M+3773$ are perfect squares. What is the units digit of $M$ ?

Answer Choices:

A. $1$

B. $2$

C. $3$

D. $6$

E. $8$

Solution:

Suppose $M+1213=j^2$ and $M+3773=k^2$ for nonnegative integers $j$ and $k$. Then

$$(k+j)(k-j)=k^2-j^2=3773-1213=2560=5\cdot 2^9$$

Because $k+j$ and $k-j$ have the same parity and their product is even, they must both be even, and it follows that one of them is $5\cdot 2^i$ and the other is $2^{9-i}$ for some $i$ with $1\le i\le 8$. Solving for $k$ gives

$$k=\frac{5\cdot 2^i+2^{9-i}}{2}$$

To maximize $M$ it is sufficient to maximize $k$, and this will occur when $i=8$ and $k=5\cdot 2^7+1=641$. Therefore $M=641^2-3773$, and its units digit is $(\text{E})\boxed{{\displaystyle 8}}$.

$$\mathbf{\text{OR}}$$

Because $(n+1{)}^2-n^2=2n+1$, successive terms in the sequence of squares, $1,4,9,16,\dots$, differ by successive odd numbers; and because $(n+2{)}^2-n^2=4(n+1)$, the terms in this sequence that are two apart differ by successive multiples of 4 . The two squares required in this problem differ by $3773-1213=2560$, a multiple of 4 . It follows that the greatest such squares are two apart in the sequence of squares, so $n+1=\frac{2560}{4}=640$. Therefore these squares are $n^2=639^2$ and $(n+2{)}^2=641^2$, and $M+1213=639^2$. Then $M=639^2-1213$, and its units digit is $(\text{E})\boxed{{\displaystyle 8}}$.

Note: Shown below is a table of $5\cdot 2^i,2^{9-i},k,j$, and $M$ for each $i$ (notation from the first solution). Observe that $M$ is maximized when $k$ is maximized.

2024 AMC 10A Problem 16

Problem:
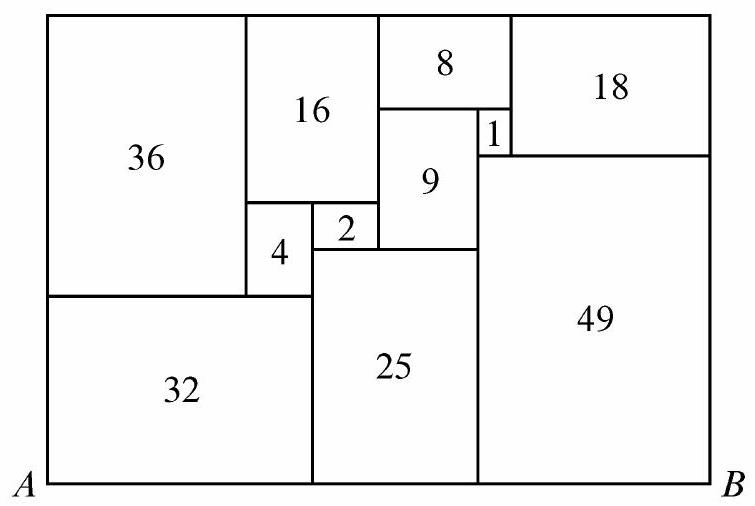
All of the rectangles in the figure below, which is drawn to scale, are similar to the enclosing rectangle. Each number represents the area of its rectangle. What is length $AB$ ?

Answer Choices:

A. $4+4\sqrt{5}$

B. $10\sqrt{2}$

C. $5+5\sqrt{5}$

D. $10\sqrt[4]{8}$

E. $20$

Solution:

Let $a$ represent the length of the shorter side of the rectangle with area 1 , and let $b$ represent the length of its longer side. Then $ab=1$, and the ratio of its long side to its short side is $\frac{b}{a}$, as is true for all of the rectangles. By similarity, the dimensions of the rectangle with area 9 are $3a$ and $3b$, and the dimensions of the rectangle with area 8 are $a\sqrt{8}$ and $b\sqrt{8}$. Because the short sides of the " 9 " and " 1 " rectangles add to the long side of the " 8 " rectangle, $a+3a=b\sqrt{8}$, and $\frac{b}{a}=\frac{4}{\sqrt{8}}=\sqrt{2}$. The area of the enclosing rectangle is the sum of the numbered areas, which is 200. Therefore $AB\cdot \frac{AB}{\sqrt{2}}=200$, so

$$AB=\sqrt{200\sqrt{2}}=\sqrt{100\sqrt{8}}=(\text{D})\boxed{{\displaystyle 10\sqrt[4]{8}}}$$

Note: This dissection was discovered by recreational mathematician Ed Pegg, Jr. The rectangles are similar to standard A4 paper.

2024 AMC 10A Problem 17

Problem:
Two teams are in a best-two-out-of-three playoff: the teams will play at most 3 games, and the winner of the playoff is the first team to win 2 games. The first game is played on Team A's home field, and the remaining games are played on Team B's home field. Team A has a $\frac{2}{3}$ chance of winning at home, and its probability of winning when playing away from home is $p$. Outcomes of the games are independent. The probability that Team A wins the playoff is $\frac{1}{2}$. Then $p$ can be written in the form $\frac{1}{2}(m-\sqrt{n})$, where $m$ and $n$ are positive integers. What is $m+n$ ?

Answer Choices:

A. $10$

B. $11$

C. $12$

D. $13$

E. $14$

Solution:

There are three ways for Team A to win the playoff: win the first two games; win the first game, lose the second game, and win the third game; or lose the first game and win the second and third games. The probability that it wins in one of these ways is

$$\frac{2}{3}\cdot p+\frac{2}{3}\cdot (1-p)\cdot p+\frac{1}{3}\cdot p^2=-\frac{1}{3}{p}^2+\frac{4}{3}p$$

Setting this equal to $\frac{1}{2}$ and simplifying gives $2p^2-8p+3=0$, and the Quadratic Formula gives solutions $\frac{1}{2}(4\pm \sqrt{10})$. Choosing the plus sign gives a nonsensical value of $p$ because it is greater than 1 , so the required probability is $\frac{1}{2}(4-\sqrt{10})\approx 0.42$. The requested sum is $4+10=(\text{E})\boxed{{\displaystyle 14}}$.

2024 AMC 10A Problem 18

Problem:
There are exactly $K$ positive integers $b$ with $5\le b\le 2024$ such that the base- $b$ integer $2024_b$ is divisible by 16 (where 16 is in base ten). What is the sum of the digits of $K$ ?

Answer Choices:

A. $16$

B. $17$

C. $18$

D. $20$

E. $21$

Solution:

Notice that $2024_b=2b^3+2b+4=2(b+1)(b^2-b+2)$, and consider the residue classes of this number modulo 8 . If $b\equiv 7(8)$, then $b+1\equiv 0(8)$, and if $b\equiv 3$ or 6 $(8)$, then $b^2-b+2\equiv 0(8)$. In each case $2024_b$ is divisible by 16 .
In all other cases $2024_b$ is not divisible by 16 . Indeed, if $b\equiv 0,2$, or $4(8)$, then $b+1$ is odd, and $b^2-b+2\equiv b+2(8)$, so $2024_b$ is divisible by no power of 2 greater than $2^3$. If $b\equiv 1$ or $5(8)$, then $b+1$ and $b^2-b+2$ are both odd multiples of 2 , so $2024_b$ is divisible by 8 , but not by 16 .
Because $2024=253\cdot 8$, there are $253\cdot 3=759$ positive integers $b\le 2024$ that are congruent to 3,6 , or 7 modulo 8 . The number 3 must be excluded from this total, because the problem statement requires $b$ to be at least 5 . Thus $K=759-1=758$, and the sum of the digits of $K$ is $7+5+8=(\text{E})\boxed{{\displaystyle 20}}$.

2024 AMC 10A Problem 19

Problem:
The first three terms of a geometric sequence are the integers $a$, 720, and $b$, where $a<720<b$. What is the sum of the digits of the least possible value of $b$ ?

Answer Choices:

A. $9$

B. $12$

C. $16$

D. $18$

E. $21$

Solution:

The prime factorization of 720 is $2^4\cdot 3^2\cdot 5$. Let $r=\frac{m}{n}$ be the common ratio of the geometric sequence, where $m$ and $n$ are relatively prime positive integers. If $n$ had any prime factor greater than 5 , then $b=720r$ would not be an integer. Analogously, if $m$ had any prime factor greater than 5 , then $a=\frac{720}{r}$ would not be an integer. It follows that $r=2^i\cdot 3^j\cdot 5^k$, where $i,j$, and $k$ are (not necessarily positive) integers. Furthermore, $\mathrm{\mid }i\mathrm{\mid }\le 4,\mathrm{\mid }j\mathrm{\mid }\le 2$, and $\mathrm{\mid }k\mathrm{\mid }\le 1$.

To minimize the value of $b$, it suffices to minimize the value of $r>1$. Taking $r=\frac{16}{15}=2^4\cdot 3^{-1}\cdot 5^{-1}$ yields the sequence $675,720,768$. To check that no lesser values of $r$ exist, first observe that $\frac{17}{16}$ is not a possible value for $r$, so both $n$ and $m$ are greater than 17 . This means that $m$ and $n$ must borrow at least two prime factors each from 720 , but 720 has only three distinct prime factors, so this is impossible. It follows that the least possible value of $b$ is 768 , and the requested sum of digits is $7+6+8=(\text{E})\boxed{{\displaystyle 21}}$.

2024 AMC 10A Problem 20

Problem:
Let $S$ be a subset of $\{1,2,3,\dots ,2024\}$ such that the following two conditions hold:

• If $x$ and $y$ are distinct elements of $S$, then $\mathrm{\mid }x-y\mathrm{\mid }>2$.
• If $x$ and $y$ are distinct odd elements of $S$, then $\mathrm{\mid }x-y\mathrm{\mid }>6$.

What is the maximum possible number of elements in $S$ ?

Answer Choices:

A. $436$

B. $506$

C. $608$

D. $654$

E. $675$

Solution:

If $S$ consists of the positive integers less than or equal to 2024 that are congruent to 1,4 , or 8 modulo 10 , then every pair of elements in $S$ differ by at least $\mathrm{\mid }4-1\mathrm{\mid }=\mathrm{\mid }11-8\mathrm{\mid }=3$, and every pair of odd elements of $S$ differ by at least $\mathrm{\mid }11-1\mathrm{\mid }=10$. This set,

$$\{1,4,8,11,14,18,\dots ,2011,2014,2018,2021,2024\}$$

satisfies the given conditions and has $3\cdot \left(\frac{2020}{10}\right)+2=(\text{C})\boxed{{\displaystyle 608}}$ elements. To see that no larger set satisfies the given conditions, note that if a set satisfies the first condition and some block of 10 consecutive integers contains 4 elements of the set, then those 4 elements would need to be the $1\mathrm{s}\mathrm{t},4$ th, 7 th, and 10th elements in that block, and the two odd numbers among them would be differ by 6 , in violation of the second condition. Therefore there are at most $3\cdot 202=606$ elements of $S$ among the first 2020 positive integers, and at most 2 elements of $S$ can be among $\{2021,2022,2023,2024\}$.

2024 AMC 10A Problem 21

Problem:
The numbers, in order, of each row and the numbers, in order, of each column of a $5\times 5$ array of integers form an arithmetic progression of length 5 . The numbers in positions $(5,5),(2,4),(4,3)$, and $(3,1)$ are $0,48,16$, and 12 , respectively. What number is in position $(1,2)$ ?

$$\left[\begin{array}{ccccc}\cdot & ?& \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & 48& \cdot \\ 12& \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & 16& \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & 0\end{array}\right]$$

Answer Choices:

A. $19$

B. $24$

C. $29$

D. $34$

E. $39$

Solution:

Let $a_{ij}$ be the integer at row $i$ and column $j$. It is given that $a_{55}=0,a_{24}=48$, $a_{43}=16$, and $a_{31}=12$. Suppose $a_{54}=d$. Then row 5 is $4d,3d,2d,d,0$ because it is an arithmetic progression with common difference $-d$. The arithmetic progression in column 1 gives

$$a_{41}=\frac{a_{31}+a_{51}}{2}=\frac{12+4d}{2}=6+2d$$

The arithmetic progression in column 4 gives

$$a_{44}=\frac{2a_{54}+a_{24}}{3}=\frac{2d+48}{3}=\frac{2}{3}d+16.$$

Row 4 gives

$$a_{43}=16=\frac{2a_{44}+a_{41}}{3}=\frac{\frac{4}{3}d+32+6+2d}{3},$$

which implies $48=\frac{10}{3}d+38$, so $d=3$. Filling in column 3 with common difference $16-6=10$ and column 1 with difference $12-12=0$ produces $a_{13}=46$ and $a_{11}=12$. Finally,

$$a_{12}=\frac{a_{13}+a_{11}}{2}=\frac{46+12}{2}=(\text{C})\boxed{{\displaystyle 29}}\mathrm{.}$$

The full array looks like this:

$$\left[\begin{array}{ccccc}12& \mathbf{29}& 46& 63& 80\\ 12& 24& 36& \mathbf{48}& 60\\ \mathbf{12}& 19& 26& 33& 40\\ 12& 14& \mathbf{16}& 18& 20\\ 12& 9& 6& 3& \mathbf{0}\end{array}\right]$$

2024 AMC 10A Problem 22

Problem:
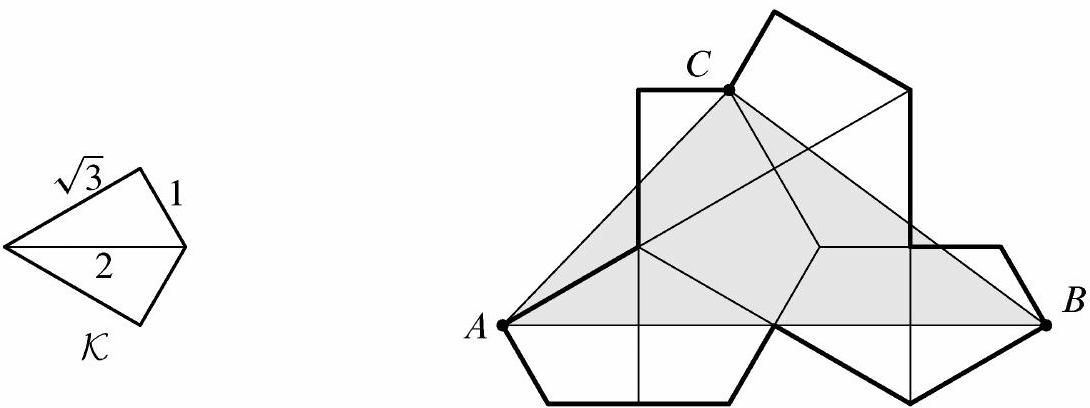
Let $\mathcal{K}$ be the kite formed by joining two right triangles with legs 1 and $\sqrt{3}$ along a common hypotenuse. Eight copies of $\mathcal{K}$ are used to form the polygon shown below. What is the area of triangle $\mathrm{△}ABC$ ?

Answer Choices:

A. $2+3\sqrt{3}$

B. $\frac{9}{2}\sqrt{3}$

C. $\frac{10+8\sqrt{3}}{3}$

D. $8$

E. $5\sqrt{3}$

Solution:

Let points $D,E,F$, and $G$ be labeled as shown. Points $A,D$, and $B$ are collinear, and the line through them is perpendicular to line $EFG$. Furthermore, the distance from $C$ to line $AB$ is equal to the distance from $E$ to line $AB$, which in turn is equal to $EG$. The area of $\mathrm{△}ABC$ is thus $\frac{1}{2}\cdot AB\cdot EG$.

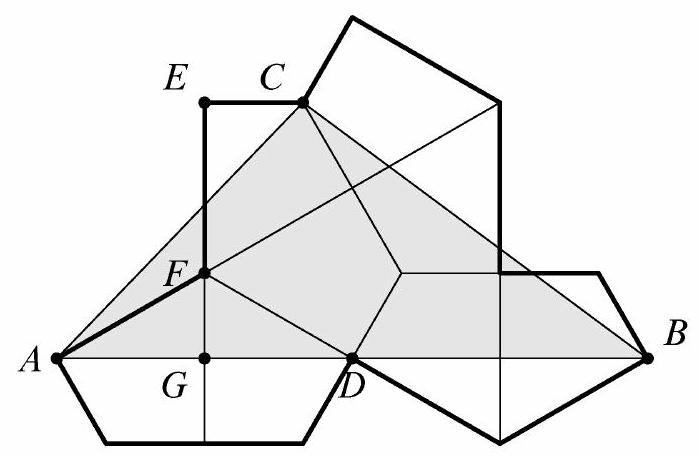
To compute $AB$, observe that $\overline{AG}$ is the longer leg of a $30-60-90^{\circ }$ triangle with hypotenuse $\sqrt{3}$. This implies that $AG=\frac{3}{2}$, from which $AB=4\cdot AG=6$. To compute $EG$, observe that in the same right triangle as before, $FG=\frac{\sqrt{3}}{2}$. This implies that $EG=EF+FG=\sqrt{3}+\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}$.\
Therefore the area of $\mathrm{△}ABC$ is $\frac{1}{2}\cdot 6\cdot \frac{3\sqrt{3}}{2}=(\text{B})\boxed{{\displaystyle \frac{9\sqrt{3}}{2}}}$.

2024 AMC 10A Problem 23

Problem:
Integers $a,b$, and $c$ satisfy $ab+c=100,bc+a=87$, and $ca+b=60$. What is $ab+bc+ca$ ?

Answer Choices:

A. $212$

B. $247$

C. $258$

D. $276$

E. $284$

Solution:

Notice that the difference between 100 and 87 is 13 , a prime number. This fact will help to simplify the problem. Subtract the second equation from the first to get

$$\begin{array}{cc}{\displaystyle 13}& {\displaystyle =(ab+c)-(bc+a)}\\ {\displaystyle }& {\displaystyle =ab-bc-a+c}\\ {\displaystyle }& {\displaystyle =b(a-c)-(a-c)}\\ {\displaystyle }& {\displaystyle =(b-1)(a-c)}\end{array}$$

Thus $b-1=\pm 1$ or $b-1=\pm 13$.

• If $b-1=-1$, then $b=0$, implying $c=100,a=87$, and $ca=60$, which is impossible.
• If $b-1=1$, then $b=2$ and $a-c=13$, implying $ca=58=2\cdot 29$,
•  which cannot be true if $a-c=13$.
• If $b-1=13$, then $b=14$ and $a-c=1$, implying $ca=46=2\cdot 23$, 
• which cannot be true if $a-c=1$.
• If $b-1=-13$, then $b=-12$ and $a-c=-1$, implying $ca=72$,
•  which is satisfied when $a=-9$ and $c=-8$. In fact, $a=-9,b=-12$, 
• and $c=-8$ satisfies all three equations.

The requested value is $ab+bc+ca=(-9)(-12)+(-12)(-8)+(-8)(-9)=108+96+72=(\text{D})\boxed{{\displaystyle 276}}$

$(-9)(-12)+(-12)(-8)+(-8)(-9)=108+96+72=(\text{D})\boxed{276}$.

Note: There are also four noninteger solutions. When written in the form $(a,b,c)$, these solutions are approximately $(0.594,0.869,99.484),(1.715,57.455,1.484),(7.477,12.525,6.349)$, and (86.214, 1.152, 0.683).

2024 AMC 10A Problem 24

Problem:
A bee is moving in three-dimensional space. A fair six-sided die with faces labeled $A^{+},A^{-},B^{+},B^{-}$, $C^{+}$, and $C^{-}$is rolled. Suppose the bee occupies the point $(a,b,c)$. If the die shows $A^{+}$, then the bee moves to the point $(a+1,b,c)$, and if the die shows $A^{-}$, then the bee moves to the point $(a-1,b,c)$. Analogous moves are made with the other four outcomes. Suppose the bee starts at the point $(0,0,0)$ and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?

Answer Choices:

A. $\frac{1}{54}$

B. $\frac{7}{54}$

C. $\frac{1}{6}$

D. $\frac{5}{18}$

E. $\frac{2}{5}$

Solution:

Without loss of generality, assume that the first roll is $A^{+}$. In order for the bee to traverse four distinct edges of a cube, the second roll cannot be $A^{+}$or $A^{-}$, so there are 4 rolls ( $B^{+}$, $B^{-},C^{+}$, and $C^{-}$) that are allowed at this stage. Each new roll must represent a perpendicular direction for the bee, and there are 3 choices that remain in compliance for the third roll-2 of which extend into three dimensions, and 1 of which creates a " C " shape. In the former case, there are 2 choices for the fourth roll, while in the latter case, there are 3 choices (including the one where the bee traverses four edges forming a square). In total, the number of compliant paths is $6\cdot 4\cdot (2\cdot 2+1\cdot 3)=$ $2^3\cdot 3\cdot 7$. The total number of paths is $6^4=2^4\cdot 3^4$, and the probability that the path represents exactly four edges of a unit cube is

$$\frac{2^3\cdot 3\cdot 7}{2^4\cdot 3^4}=\frac{7}{2\cdot 3^3}=(\text{B})\boxed{{\displaystyle \frac{7}{54}}}\mathrm{.}$$

2024 AMC 10A Problem 25

Problem:
The figure below shows a dotted grid 8 cells wide and 3 cells tall consisting of $1^{\mathrm{\prime }\mathrm{\prime }}\times 1^{\mathrm{\prime }\mathrm{\prime }}$ squares. Carl places 1 -inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?

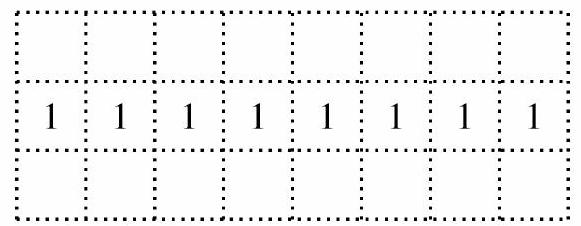
Answer Choices:

A. $130$

B. $144$

C. $146$

D. $162$

E. $196$

Solution:

There are two possibilities for the loop if it does not cross the middle row of 1 s : an $8\times 1$ rectangle around the top row of cells or an $8\times 1$ rectangle around the bottom row of cells. Otherwise, wherever the loop crosses the middle row, it must proceed straight in both directions after the middle row. This divides the dotted grid into two connected components, and both ends of the loop must enter the same connected component. It follows that the loop must cross one of the leftmost two columns and one of the rightmost two columns for a total of four configurations.

In each case there are two ends of the loop that must connect-one across the top and one across the bottom-along with some number of 1 s in the middle of the grid. Suppose there are $n$ such 1 s . For each 1 , the loop can cover either the top edge or the bottom edge. These choices are independent of each other, so the number of ways to connect both ends of the loop is $2^n$. The figure below demonstrates one possibility when $n=6$.

Of the four possibilities for what happens at the ends, one gives $n=6$, two give $n=5$, and one gives $n=4$. The total number of solutions is

$$2^6+2\cdot 2^5+2^4+2=64+64+16+2=(\text{C})\boxed{{\displaystyle 146}}$$

Note: The rules for laying matchsticks mirror those found in the logic puzzle genre Slitherlink, which originated from Japan in the early 1990s.

$$\begin{array}{cccccc}\mathbf{\text{i}}& 5\cdot 2^i& 2^{9-i}& k& j& M\\ \mathbf{\text{1}}& 10& 256& 133& 123& 13916\\ \mathbf{\text{2}}& 20& 128& 74& 54& 1703\\ \mathbf{\text{3}}& 40& 64& 52& 12& -1069\\ \mathbf{\text{4}}& 80& 32& 56& 24& -637\\ \mathbf{\text{5}}& 160& 16& 88& 72& 3971\\ \mathbf{\text{6}}& 320& 8& 164& 156& 23123\\ \mathbf{\text{7}}& 640& 4& 322& 318& 99911\\ \mathbf{\text{8}}& 1280& 2& 641& 639& 407108\end{array}$$